Inspiration
I was returning home from a late shift at the hospital, and in the subway carriage I noticed an advertisement for legal counsel regarding animal attacks. There was a phone number listed, 888 – 24 – LAW – 24, sandwiched between photos of a confident lawyer and a snarling canine.
That got me thinking, though – how do these “vanity” phone numbers work, and how difficult is it to make a sensible vanity phone number from a given phone number?

On Phone Number-Letters
Although the title of this clog is “On Phone Number-Letters,” the proper term to use is “phoneword,” defined as “mnemonic phrases represented as alphanumeric equivalents of a telephone number.” Numbers from 2 – 9 on a phone’s keypad each correspond with 3 or 4 letters of the alphabet. For example, the number “2” is equivalent to the letters “A,” “B,” or “C.” Numbers “0” and “1” are not associated with any letters.
Generally, the basis behind phonewords is marketability, and researchers have found that phonewords are more memorable to potential customers and lead to improved call rates.
For this post, I decided to take the atypical approach – generating phonewords corresponding to phone numbers, rather than choosing phone numbers corresponding to a selected phone word.
First up is converting the advertisement’s phoneword back into numbers: “LAW” is the equivalent of “529,” making the law firm’s actual phone number 888-245-2924. Not as easy to remember, right? Keeping the toll-free “888” in place, there are a total of 2,916 permutations of seven-letter words, and 20,480 permutations if one included numbers as well.
I wrote a quick and sloppy MATLAB code that took in a string of seven digits (e.g. 245-2924) and then outputted the resulting 2,916 seven-letter words. I needed to find a wordlist – although options included using the Scrabble dictionary or something like Merriam-Webster’s, I decided on a list of only commonly used words. After all, no proper vanity number would use a word that no customer would understand.
Therefore, I settled on a list of 10,000 commonly used words. From here, I filtered out words less than three or more than seven letters in length, reaching a final wordlist comprising 6,156 words. Now I was finally set, as using a simple Countif function in Excel, I was able to discover the words found within the 2,916 seven-letter words corresponding with 245-2924.
After running the script, only four words were found in the permutations of seven-letter words, and these were “jay,” “kay,” “law,” and “lay.” In selecting “law,” perhaps the dog attorneys were barking up the right tree, after all, with their vanity phone number!
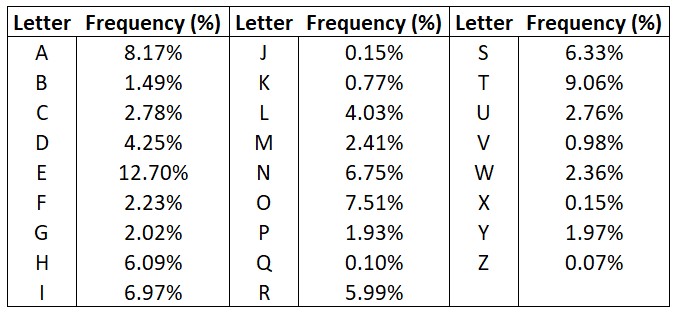
Not all phone numbers are equally suitable for vanity purposes. Recall that the numbers 0 and 1 do not correspond with any letters, so someone with a phone number containing multiple 0s and 1s would find it difficult to create a strong vanity phone number. In addition, not all letters occur with equal frequency within words. The analysis of letter frequency is a fascinating field, dating back to the 800s CE, and is often associated with cypher cracking attempts.
The frequency of English letters varies from only 0.15% for the letter X to 12.70% for the letter E, a magnitude difference of approximately 1:85. Therefore, as an aside, it is so remarkable that individuals have written books without the letter E – this sentence contains 17 Es by itself!
To determine the optimal numbers corresponding to the best odds of a sensible vanity phone number, there are three scenarios that come to mind.
1. The most straightforward option is to find consider the numbers 2 – 9 and rank them by their most frequent associated letter. If this were the case, then the following would be the respective “vanity” worth of each number (values normalized to the least vain number):
From most vain to least vain:
3 (Letter E) – 5.38
8 (Letter T) – 3.84
2 (Letter A) – 3.46
6 (Letter O) – 3.18
4 (Letter I) – 2.95
7 (Letter S) – 2.68
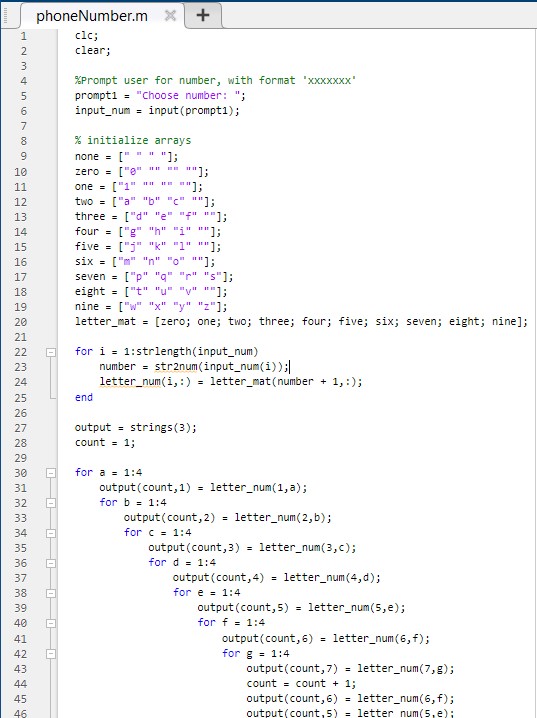
5 (Letter L) – 1.71
9 (Letter W) – 1.00
2. Another method would be to consider all of the letters represented by each number and take an average of their frequencies to determine the vanity of the number. While I cannot justify this intuition from a statistical perspective, it seems to me that that a weighted average would be a superior method for determining number vanity as compared with a simple average. However, since I have no idea of what weights I would assign to each letter, a simple average will do, yielding the following ranks:
From most vain to least vain:
3 (Letters D, E, F) – 5.62
6 (Letters M, N, O) – 4.88
4 (Letters G, H, I) – 4.42
8 (Letters T, U, V) – 3.75
2 (Letters A, B, C) – 3.65
7 (Letters P, Q, R, S) – 3.15
5 (Letters J, K, L) – 1.45
9 (Letters W, X, Y, Z) – 1.00
3. Of course, letters do not exist in isolation in words, and one should also consider common parts of words such as prefixes and suffixes. In a cryptography text called Codes & Secret Writing by Herbert Zim, the five most frequent letter pairs were, in descending order, TH HE AN RE ER, corresponding to the numbers 84 43 26 73 37.
Zim also provided the most frequent double letters – LL EE SS OO TT – equivalent to the numbers 55 33 77 66 88.
From these three scenarios, it seems likely that the vainest digit is 3 while the least vain digit is 9 followed by 5.
§
I want to address now the topic making a sensible vanity phone number from a given seven-digit phone number. Although 888-245-2924 only yielded words such as “jay” or “kay”, ill-fitting for an advertisement, the phone number contains several less vain digits such as 4, 5, and 9. Perhaps a phone number with vainer digits (e.g. 3 or 8) would yield better vanity phone numbers.
There are billions of phone numbers from all around the world that I can test, and I opted to select three phone numbers (no specific selection criteria, solely based on what crossed my mind) in New York City within where I reside: Trump Grill (212-836-3249), New York Times Square (212-452-5283), and Marwin Thai restaurant (917-675-7698). In looking for these phone numbers, I found that many prominent locations incorporate ones and zeros with high frequency; for purposes of this analysis, I decided not to select any phone numbers with either digit.
Trump Grill yielded 8 vanity phone numbers, including 212-836-3BIZ, 212-TEN-3249, and 212-836-FBI9.
New York Times Square yielded 9 vanity phone numbers, including 212-452-LATE, 212-452-KATE, and 212-45-AKA-83.
Marwin Thai Restaurant yielded 3 vanity phone numbers: 917-675-ROW-8, 917-675-ROY-8, and 917-675-SOX-8.
Based off of these three examples (admittedly a small, statistically insignificant sample size), it would appear that going from a given phone number to a useable vanity phone number is rather difficult!
Reflection
Subway station rides are great for shower thoughts – I thought about using my personal cellular phone number for this exercise, then realized that would be a foolish idea, not only because I don’t want to give out that information to the entirety of the internet, but also because the first four digits of my phone number are 2625. I’ll let you figure out what this means!

