Inspiration & Game Rules
Nothing like a game or two or five of BANANAGRAMS to get the creative word-finding juices flowing. After a handful of closely-fought series of games with a couple of friends yesterday night, I had the idea of answering the following question: how long of a word can you make on a consistent basis with a starting BANANAGRAMS hand consisting of 21 tiles?
I assume that if you are reading this post, you have a general understanding of the rules of the game. In summary, BANANAGRAMS is a tile-laying game in which the objective is to be the first to use all of one’s letters. Depending on the number of players in the game, each player begins with a set number of initial starting tiles, facedown. The remaining tiles are facedown in the middle “BUNCH.”
The game begins with one player calling out “SPLIT!” Players then simultaneously turn over their starting tiles and begin to arrange them into a word grid. This grid can be arranged as necessary throughout the game. Whenever a player places their last faceup letter into their grid, they call out “PEEL!” Every player then takes another facedown tile from the BUNCH.
If there is a particular letter tile that the player doesn’t want to use, the player can call out “DUMP!” and put that tile back, facedown in the BUNCH. However, the player must then take three more tiles from the BUNCH in exchange.
Winning occurs in the following scenario: when the number of tiles in the BUNCH is fewer than the number of players, the first person to use all their tiles in their word grid and call out “BANANAS!” wins!
B-G-A-N-A-A-M-N-R-S-A
Now, I find that BANANAGRAMS is most fun at the beginning and end of the game. At the former stage, there is a frenzy of tile-flipping and word-making as players attempt to form a word grid as fast as possible. At the latter stage, as the number of tiles in the BUNCH dwindles lower and lower, the pressure ramps up accordingly as each new tile chosen can flip over to become a letter landmine that blows up one’s chances of winning the game.

Whenever I begin a game, I aim for the longest word that jumps out immediately to mind amidst the jumble of tiles strewn across in front of me. In this game, for example, the word FRIARS was the backbone of my word grid that set me up for victory. Typically, I aim to find a word at least six to eight characters in length, such that there will be sufficient room for me to place crossing words that will branch off the main word.
At times, I find the most joy not from actually winning the game, though winning is always a nice boon, but rather from coming up with a particularly adventurous term from the starting set of tiles. A long word can set one up for success for the remainder of the game, though there is always the tradeoff with the time it takes to think of and construct such a term.
The thought then arose within my mind: how long of a word can one consistently make using the starting BANANAGRAMS tiles (21 tiles for two to four players)? Entering this analysis, my hypothesis was that one can consistently make a word at least twelve tiles in length.

I should note that the standard BANANAGRAMS set is comprised of a total of 144 tiles with a fixed number of each character of the standard A-Z English alphabet. From the BANANAGRAMMER blog, I found a nice photograph visually displaying the letter distribution.
As expected, the vowels, on average, represent a larger respective number compared with that of the consonants. Of the 144 tiles, 18 are “E,” 13 are “A,” 12 are “I,” 11 are “O,” and 6 are “U.” For the consonants, there are 9 tiles of “R” as well as “T,” and 8 tiles of “N.” With regards to the characters that one usually would hate to pick up, there are 2 tiles each of “J,” “K,” “Q,” “X,” and “Z.”
I decided to carry out a Monte Carlo simulation to account for the random drawing of the 21 initial tiles. To accomplish this, I first created a character array of 144 cells in Excel with distributions of characters corresponding to that found in the complete set. I then wrote a quick MATLAB script to randomly select the set of 21 initial tiles, without replacement, from the character array of length 144. The script used a loop to select 100 such starting sets, which I feel is a decently-sized number of runs for analysis.
I searched for some time online to find the best anagram solver for my purposes. Many of them had a clean, workable interface but had a maximum character limit of 15 or even 12. Finally, I landed on the website wordunscrambler.net that allowed for unscrambling of 21 characters! While I could have perhaps used a web crawler to automate the results, I decided to manually run through the unscrambling process 100 times to find the longest word possible for each set of starting tiles.
Now, after a few trips through the unscrambling machine, I realized that I didn’t recognize many of the words that came out on the other end – such weird words we have in the English language. As the website notes that the unscrambled words are valid in one of the “WWF, Scrabble, and other word scramble games,” I will assume that the resulting words will also be valid in BANANAGRAMS as well. I did notice that some of the words were clearly in British English (e.g. alphabetised), but we’ll let that slide!

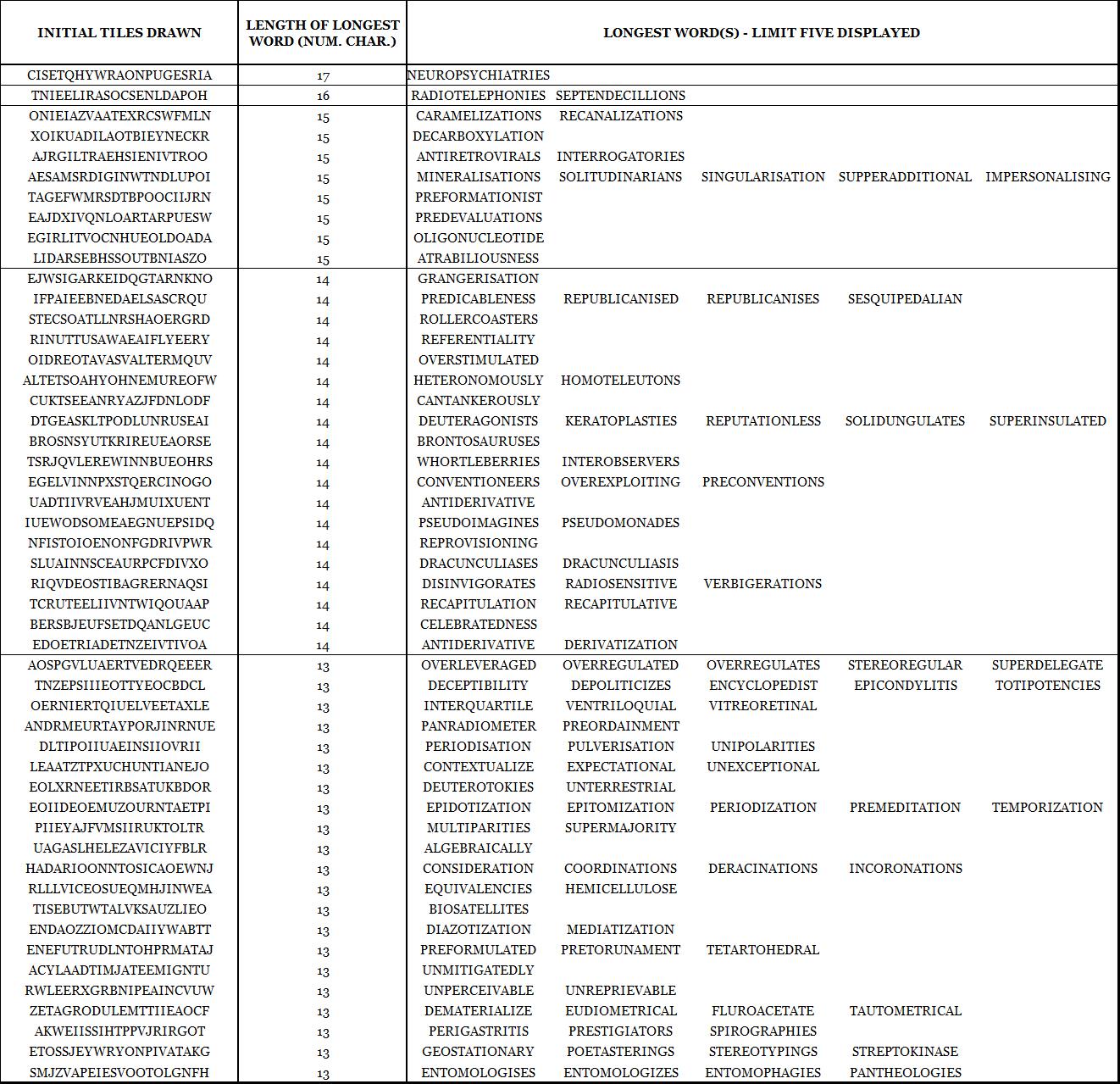
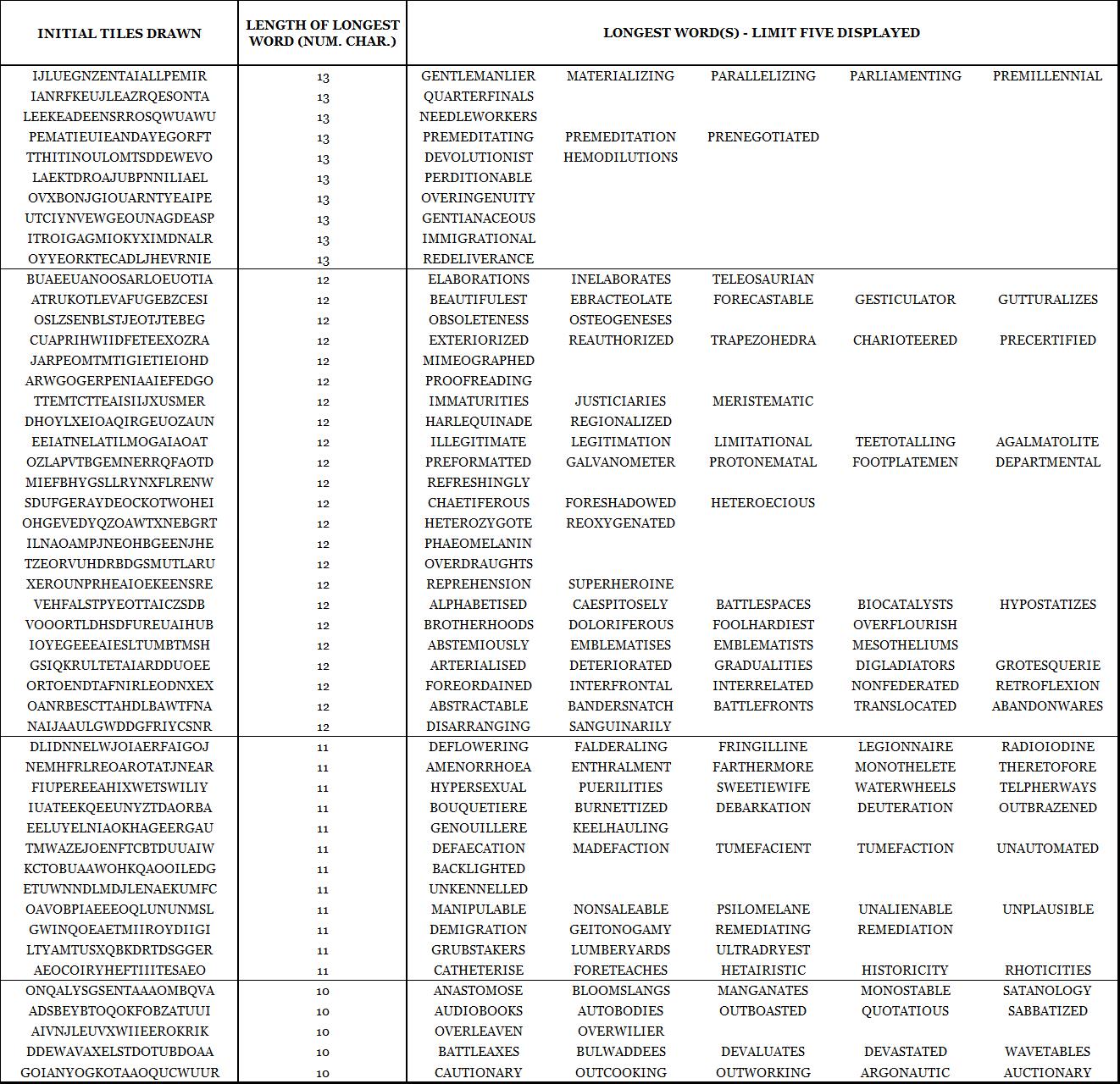
After running through the number crunching, I found that the longest word in a random draw of 21 starting tiles ranged from 10 characters to 17 characters in length (“neuropsychiatries”, drawn from the tiles CISETQHYWRAONPUGESRIA).
On average, the longest word was 12.8 characters in length. From 100 random draws, there was a 95% chance of an 11+ character word, an 83% chance of a 12+ character word, a 60% chance of a 13+ character word, a 29% chance of a 14+ character word, a 10% chance of a 15+ character word, a 2% chance of 16% character word, and a 1% chance of a 17% character word.
Based on the relative proportions of letter tiles, I also compared the average frequency of each character tile per starting hand to the expected frequency of each character tile. The comparison functions as a rough check on if I have sufficient numbers for the analysis, and it does seem like the frequencies are within a reasonable proximity in magnitude.

I know it’s probably an eyesore to see an enormous amount of long-words in tabular form, but below is the list of initial tiles along with the respective longest word(s) made. I limited the number of longest words to five per each set of initial tiles for the sake of space. If there are any mispelings [sic], know that I typed out the longest words manually, so therein lies the most likely origin of culpability.
Finally, as I come from a medical background, I wanted to highlight some of the lengthy medical terms that appeared:
Amenorrhoea
Anastomose
Antiretrovirals
Biocatalysts
Catheterise
Decarboxylation
Deuteration
Dracunculiases
Dracunculiasis
Epicondylitis
Fluroacetate
Hemodilutions
Heterozygote
Mesotheliums
Multiparities
Neuropsychiatries
Oligonucleotide
Osteogeneses
Perigastritis
Phaeomelanin
Radioiodine
Radiosensitive
Recanalizations
Reoxygenated
Retroflexion
Streptokinase
Translocated
Vitreoretinal
My guess before running the analysis was that one could consistently make a longest word of at least 12 characters in length; based on 100 runs, there is an 83% likelihood of this occurring, so my estimation was pretty spot-on!
§
Although “bananagrams” is the name of the game itself and not an actual validated word, I had another BANANAGRAMS shower thought to answer: what is the frequency of starting with a hand of 21 tiles that can spell out the ‘word’ bananagrams?
I used the same MATLAB script, modified to a simulation of 10,000 runs. Just to reiterate, from the 21 starting tiles, we’ll need at least four “A,” two “N,” and one of “B,” “G,” “R,” “M,” and “S.”
Now, glancing at the table of expected frequencies of each character per starting tiles, I think we have a small chance of this happening; essentially, one would need twice the expected frequency of “B,” “A,” “N,” “G,” “R,” and “M.” “S,” with an expected frequency of 0.88, shouldn’t be too tricky to obtain. I’ll venture that 100 out of 10,000 simulations will spell out bananagrams – a hit rate of 1%.
As there is no way to properly display a list of 10,000 sets of starting tiles, I’ll just share the findings:
Out of 10,000 simulations, there were only SEVEN simulations where a starting hand was able to spell out bananagrams. Less than 0.1% – that’s bananas!! The lucky seven sets of starting tiles are listed below – do you think you can come up with the word bananagrams in these sets of starting tiles?
ATNFBAVAOHMSROXGVUZAV
GEAALNRLMERISOWAOTEBA
VRSGAFATGDIDAXNBAMIYE
SMNNKTAIAIUZGBADRFDOA
NGIQGAFAIAOBLRISEAANM
CRMALUBNUUOAOSANHGAVP
ABATASRNEYLALMEGIIOEG
Reflection
For those who have not yet had the chance to play BANANAGRAMS, make sure to give it a try! Easy to pick up and learn, and also great exercise for the brain! Oh boy, if I ever come up with a 17-character word… I would go bananas for sure!
